- Read Me First
- Applying QoS Features Using the MQC
- 3-Level User-Defined Queuing Policy Support
- Configuring IP to ATM Class of Service
- QoS Scheduling
- QoS Hierachical Scheduling
- Legacy QoS Command Deprecation
- QoS Packet Marking
- QoS Packet-Matching Statistics Configuration
- Set ATM CLP Bit Using Policer
- EVC Quality of Service
- Quality of Service for Etherchannel Interfaces
- Aggregate EtherChannel Quality of Service
- PPPoGEC Per Session QoS
- IPv6 Selective Packet Discard
- Per ACE QoS Statistics
- QoS Packet Policing
- Queue Limits and WRED
- About
- Queue Limits
- Default Queue-Limits
- Changing Queue-Limits
- WRED
Queue Limits and WRED
About
On Cisco IOS XE devices, we dedicate memory to store packets that are queued in egress interface or QoS queues. The memory is treated as a global pool available to all interfaces rather than as carved or owned by individual interfaces.
A queue-limit caps the depth of a particular queue and serves two purposes. First, they constrain how much of the available packet memory an individual queue may consume. This ensures that other interfaces or queues also have fair access to this shared resource. Second, they constrain how much data we store if a queue is congested, thereby capping the latency applications in that queue will experience.
When a packet is ready for enqueuing we check the current depth of that queue and the configured queue-limit. If the former has already achieved the latter then the packet is dropped (tail drop).
Queue Limits
The packet memory of an ASR 1000 Series Aggregation Services Router (heretofore the ASR 1000 Series Router) is a shared resource. We do not allocate individual interfaces and queues a share of this memory. Rather they represent a global-pool available to all queues on a first come, first serve basis.
To control how much data an individual queue may store in the shared packet memory, we use queue-limit, a per-queue configurable value. It serves two purposes. First, it limits the latency for a packet arriving to a nearly full queue - at some point it is better to drop than to deliver packets so slowly that they are useless at the receiver. Second, it ensures that a single interface can’t put so many packets into the shared memory that it starves other interfaces.
We manage the shared memory very efficiently: Instead of carving pools of buffers into predetermined sizes, the hardware manages blocks of memory (32 byte blocks on the original QFP) and assigns the minimum number of blocks needed to store a packet.
The following table shows how the amount of packet memory and the maximum configurable number of queues vary by platform:
| ESP (Embedded Services Processors) Router Hardware | Packet Memory | Maximum Queues |
|
ASR1001 |
64 MB |
16,000 |
|
ASR1001-X |
512 MB |
16,000 |
|
ASR1002-F |
64 MB |
64,000 |
|
ASR1002-X |
512 MB |
116,000 |
|
ESP5 |
64 MB |
64,000 |
|
ESP10 |
128 MB |
128,000 |
|
ESP20 |
256 MB |
128,000 |
|
ESP40 |
256 MB |
128,000 |
|
ESP100 |
1 GB (two 512-MB) |
232,000* |
|
ESP200 |
2 GB (four 512-MB) |
464,000* |
For ESP100 and ESP200, physical ports are associated with a particular QFP (Quantum Flow Processor) complex on the ESP card. To maximally-use all queues, you must distributed them among different slots and SPAs in the chassis.
The amount of packet memory in an ASR 1000 Series Router is driven by a number of factors: cost, technology availability and what makes sense. When QFP was first released few choices for memory technologies were available to handle the 10s of gigabits per second of reads (and writes) required for packet memory. Even when memory could handle the speed requirements, options for size were limited and module cost was extremely high; we could have designed a system with more memory but it would have been prohibitively expensive with no real upside.
Beyond simply the number of queues supported, you must also consider the rate at which packets can ingress and egress the system. For example, looking at the ESP10, you could say that 128MB and 128,000 queues translate into 1KB of memory per queue. This is pretty meaningless if you never have all 128K queues congested simultaneously.
Let's view the size in another way: An ESP10 can transmit or receive data at a max rate of 10Gbps. At this speed, 128 MB of memory provides over 100mS of buffering which is quite reasonable.
From above it should now be evident that we expect to oversubscribe the sum of all queue-limits in the system.
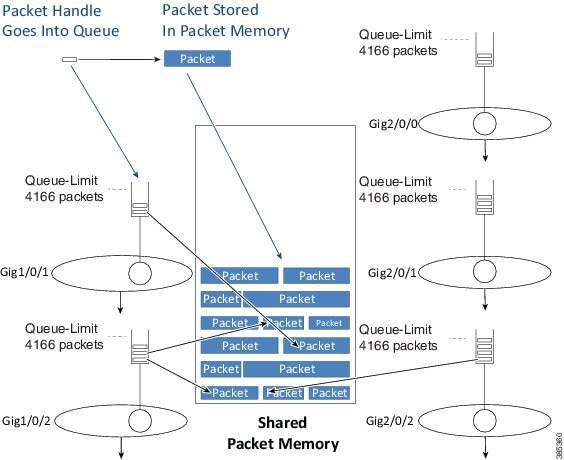
After we determine the egress interface for a packet, we will know the queue information for that interface. Into that queue we place a small packet handle, which contains the scheduling length for the packet, and a pointer to where the packet is stored in the shared packet memory. We store the actual packet itself in shared packet memory.
- Tail Drop
- Out of Resources Drop
- Memory Reserved for Priority Packets
- Vital Threshold
- Packet Mode vs Byte Mode
Tail Drop
When we enqueue a packet we first examine the configured queue-limit as well as how much data that interface currently has buffered (the instantaneous queue depth).
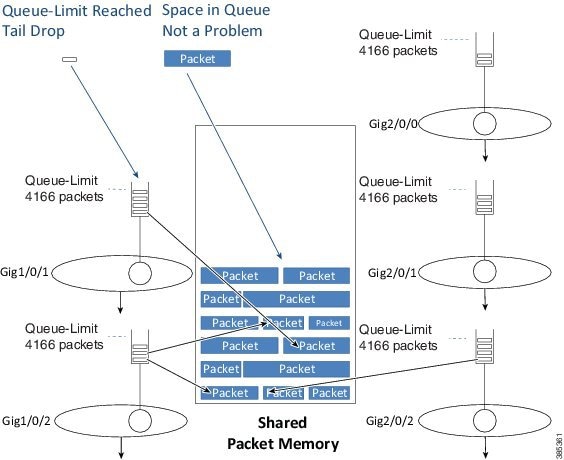
If the queue depth is already at the preconfigured limit, we will drop the packet and record a tail drop.
- If QoS is not configured, you can view the drop in the output of the show interface command.
- If QoS is configured, you can view the drop in the class output of the show policy-map interface.
As the diagram illustrates, a tail drop does not mean that no memory exists to store the packet rather it means that a queue has already reached its individual limit on how much data it can store.
Out of Resources Drop
Another scenario is possible on enqueue if the queue has not yet reached its individual queue-limit but the shared-packet memory may be full. If so and no place exists to store the packet, we must drop it. This drop would be recorded as a No Buffer drop and reported to the syslog as an Out Of Resources (OOR) condition.
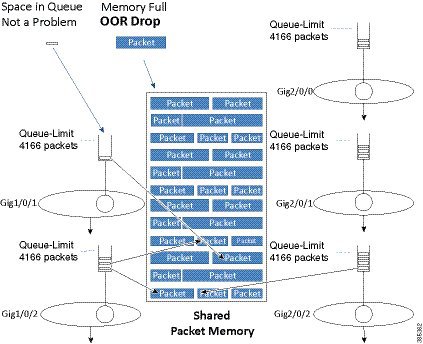
If OOR drops are only seen very occasionally you can ignore them. However, if this is a regular condition then you should review queue-limits to see whether you are allowing an individual queue or interface to consume too much memory. To avoid this situation, you might need to lower the queue-limit for one or more queues.
Memory Reserved for Priority Packets
The description of packet memory being 100% full is not really accurate. We know that some packets (those from priority classes and pak_priority packets) are more important than others and we want to ensure that we always have space in memory to store these important packets so. To do this, we limit packets from normal data queues to 85% of the total packet memory.
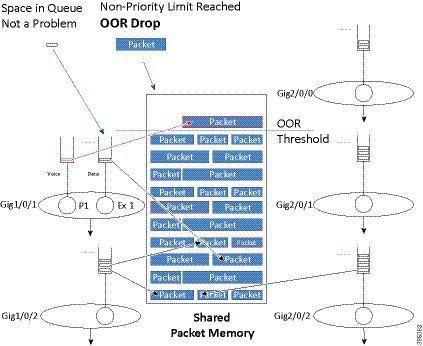
The diagram above shows how we treat priority packets and data packets differently. In this scenario, 85% of the packet memory has been consumed. If a normal data packet arrives it is dropped because the OOR threshold has been reached. However, if a priority packet were to arrive it would still be enqueued as there is physical space available.
Please note that we are not restricting priority packets to a small portion of the memory. Instead, we are dropping non-priority packets when memory is nearly full.
Vital Threshold
We also provide a second level of protection that will drop all user traffic, including priority packets, when the memory utilization exceeds 98%. We term this the vital threshold and it ensures that we can enqueue internal control packets, which are inband packets that may need to travel between different control processors in the system. As priority packets are usually forwarded when enqueued, exceeding a 98% threshold is unexpected.
You can see the amount of memory in a system and the realtime-utilization of that memory using the show platform hardware qfp active bqs 0 packet-buffer utilization command.
show platform hardware qfp active bqs 0 packet-buffer utilization
Packet buffer memory utilization details:
Total: 256.00 MB
Used : 2003.00 KB
Free : 254.04 MB
Utilization: 0 %
Threshold Values:
Out of Memory (OOM) : 255.96 MB, Status: False
Vital (> 98%) : 253.44 MB, Status: False
Out of Resource (OOR) : 217.60 MB, Status: False
On the ASR 1000 Series Aggregation Services Router, all queuing, scheduling and packet memory management is performed by dedicated hardware. When we enqueue a packet we are passing control from software to hardware. As the hardware, specifically the BQS (Buffering, Queuing and Scheduling) subsystem, manages the memory it monitors how much data each queue is currently storing in packet memory. When we are ready to enqueue a packet we query the hardware for current status. The hardware will report an instantaneous and an average queue depth for that queue. Software will then determine whether to continue with the queue or drop the packet (and report it). Tail drop decisions are made using the instantaneous queue depth reported by hardware. Instead, WRED uses the average queue depth (see Average Queue Depth).
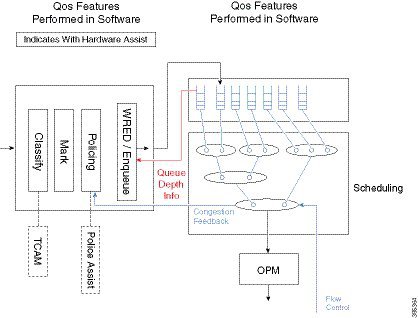
Packet Mode vs Byte Mode
The hardware may operate in one of two modes; packet mode or byte mode. When reporting the instantaneous and average queue depth it will report those values in packets or in bytes but not in both. At the time a queue is created the mode is set and can’t be changed unless you remove and reattach the policy-map.
The diagram above shows how some QoS features are performed in software and others in hardware. The enqueue is really on the boundary of the two. Software will receive Queue Depth Information from the hardware and then decide whether to drop the packet or to move it to packet memory and add a packet handle to the queue. WRED is a more advanced form of drop decision and will be covered later in the chapter.
Default Queue-Limits
The following diagram shows the need for variable queue limits.
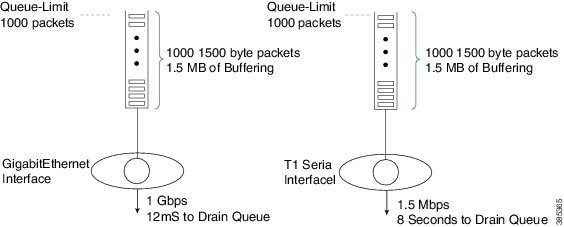
The queue on the left is serviced at 1 Gbps. If 1000 1,500 byte packets were waiting transmission it would take 12 mS to drain the queue. This means a packet arriving to an almost full queue could be delayed by 12 mS while waiting its turn to be forwarded.
The schedule on the right represents a T1 interface, a considerably slower interface operating at approx. 1.5 Mbps. If the same 1000 packets were waiting transmission through a T1 interface it would take 8 seconds to drain the queue. Obviously most users (and applications) would be disappointed with such a delay.
The diagram highlights the second role of queue-limits mentioned above - constraining the latency for applications in a queue.
How we determine the default queue mode and queue-limit will vary depending on whether or not QoS is configured.
Note that we select default queue-limits to be appropriate for as many users as possible but that does not mean they are always the best choice. We cannot know how many physical and logical interfaces will be configured in a system, how bursty traffic will be in any queue, the latency requirements of applications in a queue, etc. The defaults are a good starting point but it is not unusual to tune queue-limits further.
When Qos is not Configured
In the scheduling chapter we have seen that when no QoS is configured all packets go through a single FIFO that we refer to as the Interface Default Queue. The queue-limit for the interface default queue is configured in bytes and is calculated as 50mS worth of buffering based on the interface speed (ESP-40 is an exception where 25mS is used).
As an example consider a GigabitEthernet interface. The interface speed is 1 Gbps but with internal overdrive we send at 1.05 Gbps:
50mS worth of buffering in bytes would be: 1.05 Gbps / 8 bits per byte * .05 seconds = 6,562,500 bytes
You can use the show platform hardware qfp active infrastructure bqs queue output default interface gig1/0/0 | inc qlimit command to view the queue-limit for an interface default queue.
When QoS is Configured
 Note | The default mode for any queue created using the MQC CLI is packet. (This is an historical artifact rather than an admission that packet mode is superior.) |
Calculating queue-limit depends on a number of factors:
- If the queue is a priority queue the default queue-limit is 512 packets. Yes. This is a large limit but we assume that these values are meaningless. Because queue admission control ensures that packets are enqueued at a rate lower than they will be transmitted, a priority queue should always be nearly empty. Thus, we can set the queue-limit arbitrarily large and use it across all interface speeds.
- For a bandwidth queue we target a maximum of 50mS worth of data buffered but make an exception for low speed queues where this might represent a very small amount of data. To calculate how much data would be transmitted (in 50mS) we need to know the service speed. For an interface default queue (recall, the only game in town for scenarios without QoS) this is simple - a single queue ‘owns’ the entire bandwidth of the interface. When QoS is configured, the picture gets murky.
First, we need to introduce the concept of visible bandwidth , a value ascertained from the configuration that captures the service rate of a queue without accounting for the offered load. The table below shows how the visible bandwidth depends on the commands used:
Second, we need the Maximum Transmission Unit (MTU) for the interface where the policy is attached. As we are configuring a queue-limit in packets (recall that this is the default) and want to limit the potential latency, we look at a worst case scenario where a queue is full of MTU-size packets (view the MTU in the output of the show interface command).
Given the visible bandwidth, the MTU, and a maximum of 50mS worth of buffered data, we can calculate a queue-limit as follows:
queue-limit = (visible bandwidth / 8 bits) * 50mS / MTU
Let's consider a queue shaped to 100 Mbps on a GigabitEthernet Interface. The visible bandwidth would be the shape rate (100 Mbps) and the MTU would be 1500 bytes (what you expect on an Ethernet type interface):
queue-limit = 100 Mbps / 8 bits * .05 sec / 1500 bytes = 416 packets
As mentioned, we make an exception for low speed queues. If the calculated queue-limit is less than 64 packets we use 64 packets as the queue-limit.
Let’s consider a more comprehensive example of how to calculate default queue-limits. Consider the following hierarchical policy-map attached to a GigabitEthernet Interface:
policy-map child
class voice
priority
police cir 10m
class mission-critical
bandwidth 50000
policy-map parent
class class-default
shape average 100m
service-policy child
interface GigabitEthernet1/0/0
service-policy out parent
For completeness, the scheduling hierarchy for this policy-map would look as follows:
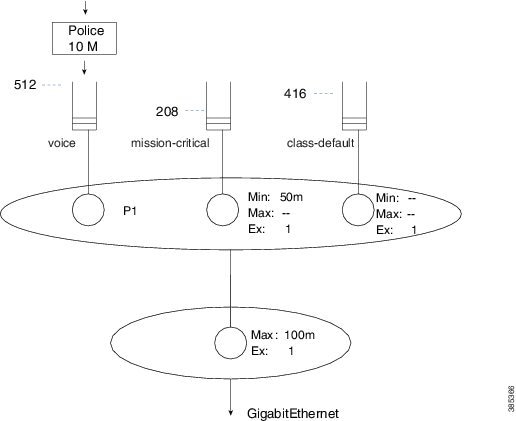
The child policy-map has three queuing classes: voice, mission-critical, and class-default. Let's examine each in turn:
The voice queue is a priority queue so queue-limit will default to 512 packets.
The mission-critical queue has the bandwidth command configured with a rate of 50 Mbps so the visible bandwidth will be 50 Mbps (refer to the table above). As this is an Ethernet-type interface the MTU is 1500 bytes:
queue-limit = 50 Mbps / 8 bits * .05 sec / 1500 bytes = 208 packets
Although the implicit class-default has no queuing command configured, the implicit excess weight is equivalent to configuring bandwidth remaining ratio 1. This means that class-default will inherit its visible bandwidth from the parent (refer to the table above). At the parent, notice the shape configured with a value of 100 Mbps. The visible bandwidth for class-default in the child is therefore 100 Mbps and as before the MTU for the interface type is 1500 bytes:
queue-limit = 100 Mbps / 8 bits * .05 sec / 1500 bytes = 416 packets
When Fair-Queue is Configured
In flow-based fair queuing we introduced flow-based fair queuing, where we configure 16 individual flow queues for a class and each flow-queue is configured with the same queue-limit. By default, this limit is ¼ of what is calculated based on the visible bandwidth of the class where the fair-queue feature is configured.
As an example, let's add fair-queue to class-default in the previous configuration example (see the asterisks):
policy-map child
class voice
priority
police cir 10m
class mission-critical
bandwidth 50000
class class-default ****
fair-queue ****
policy-map parent
class class-default
shape average 100m
service-policy child
interface GigabitEthernet1/0/0
service-policy out parent
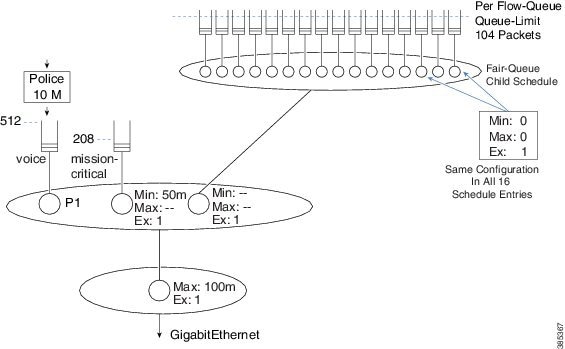
Previously we had calculated queue-limit for class-default to be 416 packets based on the visible bandwidth inherited from the shaper in the parent.
Because flow-based fair-queuing is configured, we create 16 flow queues for that one class. The queue-limit for each individual flow queue is set as 104 packets – ¼ of the 416 packets we calculated.
Changing Queue-Limits
As stated previously, the default queue-limits set by the platform should apply to the majority of users but occasionally tuning them might be required.
Why and When to Change Queue-Limits
Three general situations necessitate tuning queue-limits: OOR drops, bursty traffic leading to tail drops, and latency issues.
When you observe OOR drops, you might need to reduce queue-limits to avoid the situation. As we anticipate that each bandwidth remaining queue will inherit its visible bandwidth from the parent, OOR drops may occur when many such queues are created. Additionally, changing queue-limits to byte mode might grant more granular control over how much packet memory a given queue may consume.
Occasionally, we observe that the rate of a stream over time is less than the minimum service rate of a queue. Yet, packets are still tail dropped. You can experiment by dramatically increasing the queue-limit. If systemic oversubscription is the cause, you will tail drops no matter how large you make the queue-limit. If burstiness is causing the drops you should no longer see packet loss. A good starting point is to double the queue-limit – if drops are gone then try reduce to 1.5 times the original queue-limit. You want to find a point where drops are no longer seen but not use unreasonably large queue-limits that may in turn lead to OOR issues. Note that schedule burstiness caused by mixing very low rates with high rates in the same schedule could also be a cause.
Finally, you might need to adjust queue-limits to avoid unreasonable latency if a queue were to become congested. If you have queues with a visible bandwidth of less than roughly 15Mbps they will be assigned the default minimum queue-limit of 64 packets. If you add multiple queues to low speed interfaces, the minimum guaranteed service rates for those queues can become particularly low. Changing queue-limits to byte mode can be a good choice here.
For QoS Queue
You can use the queue-limit command to modify queue limits in any class containing a queuing action (bandwidth, bandwidth remaining, priority or shape). The queue limit may be specified in packets (default), bytes, or time. (We will review an example of each.) Here is an example of setting the limit in packet mode:
policy-map packet-mode-example
class critical-data
bandwidth percent 50
queue-limit 2000
When you use the queue-limit command with the byte option, the second option, you are changing the queue's mode from packet to byte (as discussed previously). For the change to execute, you will need to remove and reattach the policy-map (or save configuration and reload the router). If you want to specify WRED thresholds in bytes you must first use the queue-limit command to change the mode of the queue to bytes:
policy-map byte-mode-example
class critical-data
bandwidth percent 50
queue-limit 5000 bytes
 Note | If you attempt to change the queue-limit mode while a policy is attached to an interface, you will see an error message: queue-limit 5000 bytes Runtime changing queue-limit unit is not supported,please remove service-policy first |
The third option is to specify the queue limit in time (milliseconds). Actually, the hardware only supports units in either packets or bytes. When you specify the unit in milliseconds the router will convert this to bytes; you are effectively changing the mode to byte. The router will use the visible bandwidth of the class (see When QoS is Configured).
policy-map time-mode-example
class critical-data
shape average 20m
queue-limit 50 ms
In this example the visible bandwidth of the queue is 20 Mbits/sec (2.5 Mbytes/sec). In 50mS at a rate of 2.5 Mbytes per/sec, you generate 125000 bytes of data (0.05s*2.5 Mbps). Therefore, in this example, we would set queue-limit at 125000 bytes. You can verify the value calculated in the output of the show policy-map interface command.
For Interface Default Queue
You cannot directly change the queue-limit for an interface that does not have an attached QoS policy. In IOS classic, the hold-queue command achieved this. In IOS XE, the hold queue exists within the IOSd daemon but is meaningless in the regular packet forwarding path. However, adjusting the hold-queue still has meaning for packets punted to IOSd, provided you have a topology with a very large number of routing peers and require more buffering within IOSd to handle simultaneous updates from all those peers.
To change the queue limit for the interface default queue, you can attach a simple policy-map with just class-default:
policy-map modify-interface-queue
class class-default
queue-limit 100 ms
!
interface gigabitethernet1/0/0
service-policy out modify-interface-queue
WRED
WRED is a feature that monitors queue utilization. Under congestion and to alleviate further congestion, it randomly drops packets signaling endpoints to reduce their transmission rate.
- Relience on Elasticity of IP Flows
- The How of WRED
- Average Queue Depth
- WRED Threshholds and Drop Curves
- WRED - Changing Drop Curves
- WRED Max Thresholds for Priority Enqueue
- ECN - Explicit Congestion Notification
- Mode: Precedence, DSCP, and Discard-Class
Relience on Elasticity of IP Flows
WRED relies on the elasticity of many IP flows, where elastic describes flows that increase and reduce their send rate when the receiver detects missing packets. A very good example of elasticity is TCP. It starts slowly then increases the sender’s congestion window (amount of outstanding unacknowledged traffic allowed) until either it reaches the maximum receiver's receive window size or it loses packets in the network. If the latter, it switches to a congestion avoidance algorithm, attempting to settle at the maximum congestion window size achievable without losing packets (see RFC 5681 for further details).
Another good example of elastic traffic is video (consider your favorite video streaming application). After starting the video, you typically observe that video quality improves as the rate increases. The rate continues to increase until the application discerns the capacity of the network. When it detects drops in the network it will recede, delivering the highest quality possible given the prevailing network conditions.
The How of WRED
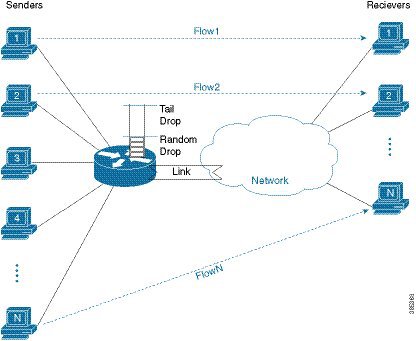
With the diagram above, we visualize how WRED operates.
Senders behind our router send traffic to receivers elsewhere in the network. WRED is configured on the link (interface) connecting the router to the network. When the sum of the send rates of all the flows exceeds the link capacity we observe packets backing up in the queue configured for that interface.
In the section Tail Drop, we described a tail-drops threshold for a queue. WRED uses a lower (minimum) threshold to determine when congestion is occurring. When the queue-depth reaches this threshold, we randomly drop packets rather than enqueue them, despite the queue spaces that are still available. The random nature of the drops ensures that we only drop packets from a small number of flows.
Let's say that you initially drop a single packet from Flow 1. TCP (or whatever elastic transport mechanism) will detect that drop and reduce the send rate of that flow. If by doing so, the link rate now exceeds the aggregate send rate, then the queue depth will start to fall. If the queue depth falls below the WRED minimum threshold then WRED will cease dropping packets.
If the aggregate send rate still exceeds the link rate then the queue depth will continue to increase and WRED will continue to randomly drop packets. What if we now drop a packet from Flow 4, both Flows 1 and 4 are now backed off. This process continues until enough streams back off to alleviate the congestion.
The random element of WRED ensures that not all flows back off at the same time. If they did, they would likely try to increase their send rates again at the same time, resulting in a saw tooth effect where in synchrony, all senders reduce and increase their send rates. By randomly selecting packets to drop we randomly signal that different flows should back off at different times.
Average Queue Depth
In the previous discussion of WRED, we described random drops occurring when the queue depth crossed a predetermined threshold. Actually, we use a dampened average of the queue depth rather than the instantaneous queue-depth, which we use for the tail drop check and average queue depth for WRED.
Surely, this is no surprise: internet traffic is bursty. If we used instantaneous queue depth to monitor congestion we might drop packets in haste and so respond to normal bursts in traffic rather than to real congestion.
To determine how changes in average queue depth are dampened, we use the WRED Exponential Weighting Constant. The router will remember the current value of average queue depth. Whenever a packet reaches the enqueue stage, we examine the instantaneous queue depth and recalculate the average queue depth. The formula to calculate the new value of average queue depth is as follows:
Avg = OldAvg + (Instantaneous-OldAvg)/2^exp-weighting-constant
where Avg is the average queue depth calculated at the current enqueue time; Instantaneous, the current queue depth; and OldAvg, the previously calculated average that we remembered since the last enqueue.
For example, if the OldAvg is 12.0 packets, the Instantaneous is 14 packets (observed upon enqueuing a packet), and exp-weighting-constant is 6 (the default for packet mode WRED on the ASR 1000 Router), the Avg would be:
Avg = 12 + (14 – 12) / 2^6 = 12 + .03125 = 12.03125
 Note | exp-weighting-constant = 9 if the queue is run in byte mode. |
Later, we enqueue another packet. If one packet was transmitted from the head of the queue in the interim, the instantaneous queue depth would remain 14. Now, the calculation of AVG yields:
Avg = 12.03125 + (14 – 12.03125)/2^6 = 12.03125 + 0.0308 = 12.06201
The example shows that the average queue depth is dampened. The instantaneous queue depth can grow considerably beyond the average. Consequently, the WRED max threshold is always considerably less than the queue limit. The example also illustrates the time necessary for the average to converge on the instantaneous, even if the queue depth stays consistent for some time. This dampening of average queue depth is how WRED avoids reacting to regular microbursts in traffic.
Only with a PHd in voodoo mathematics, should you consider changing the value of EWC. It is a "true geek knob" that should be avoided. For completeness only and not to encourage, here is the code change the EWC:
policy-map ewc-example
class class-default
random-detect
random-detect exponential-weighting-constant 5
WRED Threshholds and Drop Curves
WRED drop decisions are driven by the average queue depth calculated upon enqueue.
When configuring WRED, we set a Minimum threshold, a Maximum threshold, and a Drop Probability for each precedence value (or DSCP, discard-class, etc.).
The following diagram shows the drop curve for a sample precedence value.
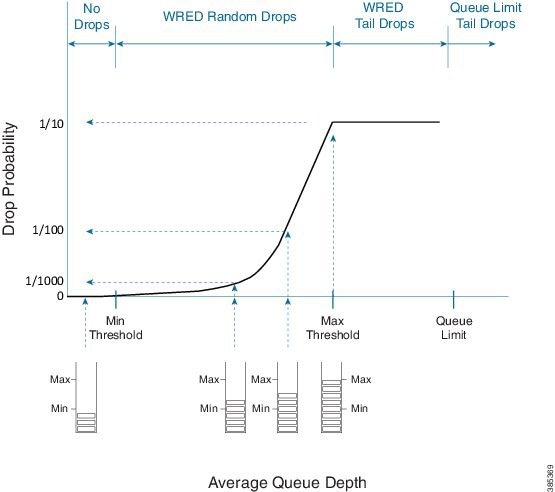
If the average queue depth is calculated to a value less than the WRED minimum threshold we are in a range where WRED will not drop any packets.
Between the Min and Max thresholds we are in the WRED random drop zone. Observe the exponential rise in drop probability from zero at the Min threshold to the configured WRED drop probability (defaults to 1 in 10 packets) at the Max threshold. The exponential nature of the curve means WRED will drop a very small number of packets when the average queue depth approximates the minimum threshold. As the illustration as reflects, the average queue depth and drop probability increase in tandem. Knowing the average queue depth, we know the associated drop probability. Then, we decide whether to drop the packet or enqueue it.
If the WRED average queue depth is calculated to exceed the maximum threshold then the packet will experience a WRED tail drop. This differs slightly from the queue-limit tail drop - it is driven by average rather than instantaneous queue depth. If the instantaneous queue depth reaches the class’s queue limit then the drop would be recorded as a queue-limit tail drop as opposed to a WRED tail drop.
Please note that the ‘W’ in WRED stands for weighted (some traffic may be dropped more aggressively than others).
Here, we show how to use multiple drop curves:
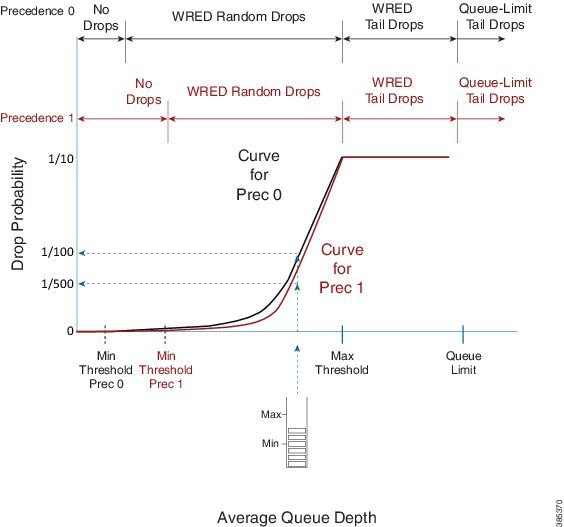
If a packet with IP precedence 0 arrives, the router will apply the black curve to calculate the drop probability. In the example the drop probability is calculated as 1 in 100 packets.
If a packet with IP precedence 1 arrives, we apply the mauve-colored curve. For the same average queue depth we would now see a drop probability of just 1 in 500.
Notice how the default maximum threshold is the same for each precedence value. The difference in WRED minimum threshold for each precedence value means that we will start dropping precedence 0 traffic before we drop any other traffic. Moreover, we will be more aggressive in dropping that traffic for a given queue depth in the random drop zone.
 Note | When you configure WRED, for each drop curve, the router will pick appropriate values for Min threshold, Max threshold and Drop Probability. Those values depend on the configured queue limit thereby accounting for the interface speed. We strongly recommend that you use the default values unless you fully understand the implications of any change. |
WRED - Changing Drop Curves
Regardless of the WRED mode, you can tune any individual drop curve. Using the same command you may change the Minimum Threshold, the Maximum Threshold or the Drop Probability at Maximum Threshold for that drop curve. With the minimum and maximum thresholds and the drop probability, a router can construct the exponential curve it needs to determine drop probability for any average queue depth. Tuning WRED parameters is not typical; do not attempt unless you have a thorough understanding of how tuning will impact applications in that class. The default values should suffice for the vast majority of use cases.
If you decide to tune WRED drop curves, you have the option to specify thresholds in packets (default), bytes or time. The queue-limit must be configured in the chosen unit before you add WRED configuration to the class and only when the queue is already running in the desired mode can you change thresholds in that unit. Moreover, you can only change the curve for a particular DSCP, precedence or discard-class value provided WRED is operating in that mode.
Recall that the drop probability is an integer number. If the average queue limit is at the maximum threshold, a packet has a 1 in that integer value chance of being dropped. For example, if the drop probability is 20, a 1 in 20 (5%) chance exists for a packet to dropped by WRED.
The command to change a drop curve is random-detect [dscp|precedence|discard-class] value min-threshold max-threshold drop-probability, as illustrated here:
policy-map tuneprecedence
class bulk-data
bandwidth remaining percent 30
random-detect
random-detect precedence 1 1301 2083 10
Running the queue in packet mode (the default) and WRED in precedence mode (also the default), I decide against differentiation in the minimum threshold for precedence 1 and 2. I change the curve for precedence 1, setting the minimum threshold to 1301, the maximum threshold to 2083 and the drop probability at max threshold to 1 in 10 packets:
random-detect precedence 1 1301 2083 10
As always, we can verify the configuration with the show policy-map interface command:
show policy-map interface g1/0/0
GigabitEthernet1/0/0
Service-policy output: tuneprecedence
Class-map: bulk-data (match-all)
0 packets, 0 bytes
5 minute offered rate 0000 bps, drop rate 0000 bps
Match: access-group name bulkdata
Queueing
queue limit 4166 packets
(queue depth/total drops/no-buffer drops) 0/0/0
(pkts output/bytes output) 0/0
bandwidth remaining 30%
Exp-weight-constant: 4 (1/16)
Mean queue depth: 1086 packets
class Transmitted Random drop Tail drop Minimum Maximum Mark
pkts/bytes pkts/bytes pkts/bytes thresh thresh prob
0 0/0 0/0 0/0 1041 2083 1/10
1 0/0 0/0 0/0 1301 2083 1/10
2 0/0 0/0 0/0 1301 2083 1/10
3 0/0 0/0 0/0 1431 2083 1/10
4 0/0 0/0 0/0 1561 2083 1/10
5 0/0 0/0 0/0 1691 2083 1/10
6 0/0 0/0 0/0 1821 2083 1/10
7 0/0 0/0 0/0 1951 2083 1/10
Notice the new values we set for precedence 1.
What if we change the thresholds for a queue that is running in time-based mode where WRED is running in DSCP mode? In particular, we want the minimum threshold of af21 to exceed that of af11. The configuration would appear as follows:
policy-map tunedscp
class bulk-data
bandwidth remaining percent 30
queue-limit 50 ms
random-detect dscp-based
random-detect dscp af21 22 ms 25 ms 10
Looking at the output of show policy-map interface we verify the configuration:
show policy-map interface g1/0/0
GigabitEthernet1/0/0
Service-policy output: tunedscp
Class-map: bulk-data (match-all)
148826 packets, 223239000 bytes
5 minute offered rate 2358000 bps, drop rate 0000 bps
Match: access-group name bulkdata
Queueing
queue limit 50 ms/ 6250000 bytes
(queue depth/total drops/no-buffer drops) 0/0/0
(pkts output/bytes output) 148826/223239000
bandwidth remaining 30%
Exp-weight-constant: 9 (1/512)
Mean queue depth: 0 ms/ 992 bytes
dscp Transmitted Random drop Tail drop Minimum Maximum Mark
pkts/bytes pkts/bytes pkts/bytes thresh thresh prob
ms/bytes ms/bytes
af11 96498/144747000 0/0 0/0 21/2734375 25/3125000 1/10
af21 52328/78492000 0/0 0/0 22/2750000 25/3125000 1/10
With DSCP-based WRED we will only show curve statistics for DSCP values that have been observed within that class (refer to Mode: Precedence, DSCP, and Discard-Class).
WRED Max Thresholds for Priority Enqueue
In the WRED - Changing Drop Curves, we showed how to tune the minimum threshold of WRED curves. Another option is to modify the maximum threshold. When you do so with different thresholds for different DSCP values you can effectively claim that under congestion we always drop one type of traffic.
Let's use af11 to designate in-contract bulk data traffic and af12 to designate out-of-contract bulk data traffic? Under congestion, we want to always provide preferential treatment to af11 over af12. If we specify a lower WRED maximum threshold for af12 we could drop this traffic while still enqueuing af11.
In the following configuration, we change the maximum threshold for af12 from the default of 624 packets (for this bandwidth) to 580 packets:
policy-map maxthreshold
class bulk-data
bandwidth percent 30
random-detect dscp-based
random-detect dscp af12 468 580 10
Let's verify the configuration:
show policy-map interface g1/0/0
GigabitEthernet1/0/0
Service-policy output: maxthreshold
Class-map: bulk-data (match-all)
359826 packets, 539739000 bytes
5 minute offered rate 7208000 bps, drop rate 0000 bps
Match: access-group name bulkdata
Queueing
queue limit 1249 packets
(queue depth/total drops/no-buffer drops) 0/0/0
(pkts output/bytes output) 359826/539739000
bandwidth 30% (300000 kbps)
Exp-weight-constant: 4 (1/16)
Mean queue depth: 0 packets
dscp Transmitted Random drop Tail drop Minimum Maximum Mark
pkts/bytes pkts/bytes pkts/bytes thresh thresh prob
af11 154689/232033500 0/0 0/0 546 624 1/10
af12 205137/307705500 0/0 0/0 468 580 1/10
Looking at the configuration you can see that if the average queue depth exceeds 580 packets, all af12 packets would be WRED tail dropped but we would still enqueue af11 packets.
Be alert when modifying maximum thresholds to ensure that behavior is as expected. Here, if congestion persists and the average queue depth remains above 580 packets, then we would totally starve af12 traffic of any service during persistant congestion.
ECN - Explicit Congestion Notification
Explicit Congestion Notification (ECN) is an extension to the IP protocol where the network can mark a packet to signal congestion to the endpoints rather than drop packets early to signal congestion. Upon receiving such a packet, the endpoint echoes that congestion notification back to the sender.
 Note | ECN mode must be explicitly enabled in WRED. |
To understand ECN you should first grasp the TOS byte in the IP header. Originally it was used to carry IP precedence bits in the 3 most significant bits, and more recently, to carry the DSCP codepoint in the 6 most significant bits of this byte. We define the remaining 2 bits in RFC3168 as ECN bits.
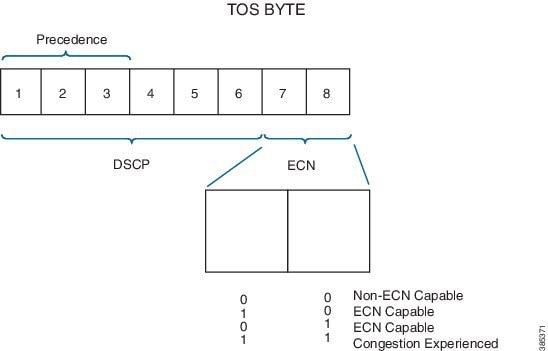
When WRED is configured in ECN mode it will look at the ECN bits before dropping a packet. If these bits are both set to zero, the router assumes the endpoints are ECN incapable and WRED will drop the packet to signal congestion is occurring.
If either of the ECN bits is set to 1, the router assumes that the endpoint is ECN capable and can mark congestion experienced rather than dropping the packet by setting both ECN bits to 1. The endpoints must signal a transport is ECN capable only if the upper layer protocol is elastic in nature.
 Note | The router will only look at the ECN bits when determining whether to mark or drop a packet. |
The following is an example of configuring WRED in ECN mode:
policy-map ecn-example
class bulk-data
bandwidth remaining percent 30
random-detect dscp-based
random-detect ecn
Mode: Precedence, DSCP, and Discard-Class
WRED Precedence Mode
In WRED Threshholds and Drop Curves we describe drop curves.
When you enable WRED the default is to run in precedence mode and create 8 distinct drop curves, one for each valid precedence value. The default minimum threshold increases with the precedence value. The impact is that precedence 0 will start dropping earlier and more aggressively than precedence 1, precedence 1 earlier and more aggressively then precedence 2, etc. The same default maximum threshold and drop probability is configured for each curve.
When a packet arrives the IP precedence bits determine which curve we use to find the appropriate drop probability. If the packet is not "IP," we use the precedence 0 drop curve. If the packet is MPLS encapsulated then the EXP bits are treated as precedence bits and determine the appropriate drop curve.
In the following example we enable WRED in precedence mode. Observe that WRED must reside in a class that has a queuing action (including class-default):
policy-map wred-precedence-example
class bulk-data
bandwidth remaining percent 30
random-detect
random-detect precedence-based
In this example, we use bandwidth remaining command as the queuing action. The random-detect command enables WRED in the class bulk-data and the random-detect precedence-mode command tells WRED to operate in precedence mode.
 Note | The random-detect precedence-mode command is optional as the default mode for WRED is precedence-based. |
As with all QoS features the show policy-map interface command is the primary means to verify your configuration:
show policy-map int g1/0/0
GigabitEthernet1/0/0
Service-policy output: wred-precedence-example
Class-map: bulk-data (match-all)
6468334 packets, 9702501000 bytes
5 minute offered rate 204108000 bps, drop rate 0000 bps
Match: access-group name bulkdata
Queueing
queue limit 4166 packets
(queue depth/total drops/no-buffer drops) 1308/0/0
(pkts output/bytes output) 6468335/9702502500
bandwidth remaining 30%
Exp-weight-constant: 4 (1/16)
Mean queue depth: 1308 packets
class Transmitted Random drop Tail drop Minimum Maximum Mark
pkts/bytes pkts/bytes pkts/bytes thresh thresh prob
0 0/0 0/0 0/0 1041 2083 1/10
1 0/0 0/0 0/0 1171 2083 1/10
2 0/0 0/0 0/0 1301 2083 1/10
3 0/0 0/0 0/0 1431 2083 1/10
4 6468335/9702502500 0/0 0/0 1561 2083 1/10
5 0/0 0/0 0/0 1691 2083 1/10
6 0/0 0/0 0/0 1821 2083 1/10
7 0/0 0/0 0/0 1951 2083 1/10
Notice how statistics and curve configuration values are displayed for each of the 8 drop curves that are created in precedence mode. The average queue-depth is less than the minimum threshold so no random drops are reported.
WRED DSCP Mode
The second option for configuring WRED is DSCP mode, where we create 64 unique curves.
Similar to precedence mode, any non-IP traffic will use the default (DSCP 0) curve. If MPLS traffic is seen, we treat the MPLS EXP bits as precedence values and select the curve accordingly (EXP 1 treated as DSCP CS1, EXP 2 as CS2, etc.).
Here is an example of configuring WRED in DSCP mode:
policy-map wred-dscp-example
class bulk-data
bandwidth remaining percent 30
random-detect dscp-based
Here, we verify the configuration with the show policy-map interface command:
show policy-map int
GigabitEthernet1/0/0
Service-policy output: wred-dscp-example
Class-map: bulk-data (match-all)
5655668 packets, 8483502000 bytes
5 minute offered rate 204245000 bps, drop rate 0000 bps
Match: access-group name bulkdata
Queueing
queue limit 4166 packets
(queue depth/total drops/no-buffer drops) 0/0/0
(pkts output/bytes output) 5655669/8483503500
bandwidth remaining 30%
Exp-weight-constant: 4 (1/16)
Mean queue depth: 1 packets
dscp Transmitted Random drop Tail drop Minimum Maximum Mark
pkts/bytes pkts/bytes pkts/bytes thresh thresh prob
af11 1205734/1808601000 0/0 0/0 1821 2083 1/10
cs4 5270109/7905163500 0/0 0/0 1561 2083 1/10
Notice that we only display statistics and drop curve information for 2 DSCP values (af11 and cs4). In DSCP mode, 64 unique drop curves are configured and IOS will maintain statistics for all. However, it will only display information for drop curves that have actually observed traffic. In this example, we have observed only display traffic with DSCP af11 and cs4, hence the display.
WRED Discard-Class
Discard-class is an internal marking very similar in concept to qos-group. We can mark discard-class on ingress (and not on egress) as well as employ to select a WRED drop curve on egress.
Occasionally, the precedence or DSCP marking in a packet is unavailable for classification on an egress interface. A use-case is an MPLS-encapsulating router where we receive IP packets on the ingress interface and forward MPLS-encapsulated packets on the egress interface.
DSCP must be mapped into a smaller number of EXP values (6 bits in the DiffServ field vs 3-bit field in MPLS header) so some granularity is lost. Let's say af11 is used for in-contract and af12 for out-of-contract bulk data. On the egress interface the DSCP visibility is lost; af11 and af12 would probably be mapped into the same EXP. Now, what if we want to provide preferential treatment to af11 over af12 on the egress interface?
We could use WRED discard-class mode to achieve this. To do so, you will need to mark discard-class on ingress interfaces, as in the following sample policy:
policy-map mark-in-contract
class bulk-data
police cir 50000000 pir 100000000
conform-action set-dscp-transmit af11
conform-action set-mpls-exp-imposition-transmit 1
conform-action set-discard-class-transmit 2
exceed-action set-dscp-transmit af12
exceed-action set-mpls-exp-imposition-transmit 1
exceed-action set-discard-class-transmit 1
violate-action drop
conform-action set-dscp-transmit af11
conform-action set-mpls-exp-imposition-transmit 1
conform-action set-discard-class-transmit 2 ****
exceed-action set-dscp-transmit af12
exceed-action set-mpls-exp-imposition-transmit 1
exceed-action set-discard-class-transmit 1 ****
Violating traffic is dropped.Notice how the same EXP value will be set for conforming and exceeding traffic – it is all bulk data traffic and will use the same per-hop-behavior in the MPLS network. However, for in-contract and out-of-contract traffic we also mark distinct discard-classes (see the asterisks), which we use use on the egress interface to provide preferential treatment.
On the egress interface you would configure WRED in discard-class-based mode, as follows:
policy-map wred-discard-class-example
class bulk-data
bandwidth remaining percent 30
random-detect discard-class-based
Looking at the output of show policy-map interface command you will see something like:
show policy-map int g1/0/0
GigabitEthernet1/0/0
Service-policy output: wred-discard-class-example
Class-map: bulk-data (match-all)
1500 packets, 1040000 bytes
5 minute offered rate 51955000 bps, drop rate 0000 bps
Match: access-group name bulkdata
Queueing
queue limit 4166 packets
(queue depth/total drops/no-buffer drops) 943/0/0
(pkts output/bytes output) 1500/1040000
bandwidth remaining 30%
Exp-weight-constant: 4 (1/16)
Mean queue depth: 943 packets
discard-class Transmitted Random drop Tail drop Minimum Maximum Mark
pkts/bytes pkts/bytes pkts/bytes thresh thresh prob
0 0/0 0/0 0/0 1041 2083 1/10
1 500/4000 0/0 0/0 1171 2083 1/10
2 1000/1000000 0/0 0/0 1301 2083 1/10
3 0/0 0/0 0/0 1431 2083 1/10
4 0/0 0/0 0/0 1561 2083 1/10
5 0/0 0/0 0/0 1691 2083 1/10
6 0/0 0/0 0/0 1821 2083 1/10
7 0/0 0/0 0/0 1951 2083 1/10
Looking at the output you can see that 8 drop curves are created when you run WRED in discard-class mode. Referring to the configuration above, in-contract traffic is marked with discard-class 2 and out-of-contract traffic is marked with discard-class 1.
You can also see that the WRED curve for discard-class 1 has a lower minimum threshold. This means that under congestion, out-of-contract traffic will start dropping earlier and more aggressively than in-contract traffic.
Any traffic devoid of an explicitly-set discard-class is assumed to that does not have a discard-class explicitly set will be assumed to be discard-class 0.
Command Reference - random detect
Use the random-detect options command to enable and control operation of WRED, applying different options as below.
- Enable WRED in precedence mode.
random-detect precedence-based
- Enable WRED in precedence mode.
random-detect dscp-based
- Enable WRED in DSCP mode.
random-detect discard-class-based
- Enable WRED in discard-class mode.
- Modify the drop curve for a particular precedence value
- Modify the drop curve for a particular DSCP value
- Modify the drop curve for a particular discard-class value. Note the min-threshold and max-threshold may be configured in packets (default), bytes or time. To use the units of bytes or time the queue must first be configured for that mode using the queue-limit command.
- random-detect exponential-weighting-constant value
- random-detect ecn
The random-detect command may be used in any queuing class configured with the bandwidth, bandwidth remaining or shapecommands. This includes class-default which has an implicit bandwidth remaining value.
The ASR 1000 Series Aggregation Services Router has no queues in parent or grandparent levels of a scheduling hierarchy. So, the random-detect command is not supported in any class that contains a child queuing policy.
The default values for WRED minimum and maximum thresholds are proportional to the queue-limit for a class and therefore proportional to the expected service rate of the queue. Modifying WRED drop curves should not be undertaken unless you have a deep understanding on how changes will affect applications in that class.
 Feedback
Feedback