Post Quantum Security Brief

 

Introduction

In networking and communication, information security is absolutely necessary when transmitting over any untrusted medium, especially the Internet. Interestingly, people have been trying to securely encrypt information for 1000s of years, mostly using intuitive methods of encrypting, which is a good reason why we need cryptography. Cryptography protects data from being stolen or altered and is also used for individual authentication. There are three types of cryptographic schemes typically used to accomplish these goals: secret key (or symmetric) cryptography, public-key (or asymmetric) cryptography, and hash functions.

There is some confusion and noise in the communications market on post-quantum security threats. This paper is an attempt to provide some clarity on the issues and the possible solutions and demonstrate how Cisco is preparing in this new era.

The Problem

Cryptography is used today to protect information over a public channel between two entities. The most common algorithms used are symmetric keys, which means both ends of the channel use the exact same key to encrypt and decrypt the message being sent.

Because a symmetric algorithm requires each end to have the same key, we need a way to get the same secret key to both sides. Either they are preprovisioned with the same key, or you need another algorithm to transport the key from one side to the other. An asymmetric algorithm is where there is a public key and a private key – everyone uses the public key to encrypt but only if someone has the private key can they decrypt the message. While there are many good asymmetric algorithms, they are all a computationally heavy way to approach the problem. To simplify, communication equipment commonly uses the asymmetric algorithm to distribute keys and a symmetric algorithm for the actual transmission.

One can also use a digital signature, which is another algorithm validating that the message coming in is really from the expected sender. A digital signature is also based on a private and a public key; the private key allows someone to “sign” the message, and the public key allows someone to validate that the signed message is exactly as the signer intended (but importantly, the public key does not allow you to sign any message).

The problem is that the most common algorithms used for both public key encryption and digital signatures are likely to be broken by a large enough quantum computer.

The Solution

Physics proposed a solution known as Quantum Key Distribution (QKD; the most famous is the Bennett-Brassard 1984 protocol), which uses the quantum property of the particle to create and transmit a secure key. This is an interesting solution because a quantum particle state cannot be copied, so it is inherently possible to validate that a transmitted key is secure.

To understand quantum computing power and quantum key distribution, we need first to explain the qubit and entanglement concepts. In quantum mechanics, a qubit is a basic unit of quantum information (the quantum version of the classical binary bit).

Qubits, differently from classic bits, might be in a so-called coherent superposition of more states. Let’s see what this means.

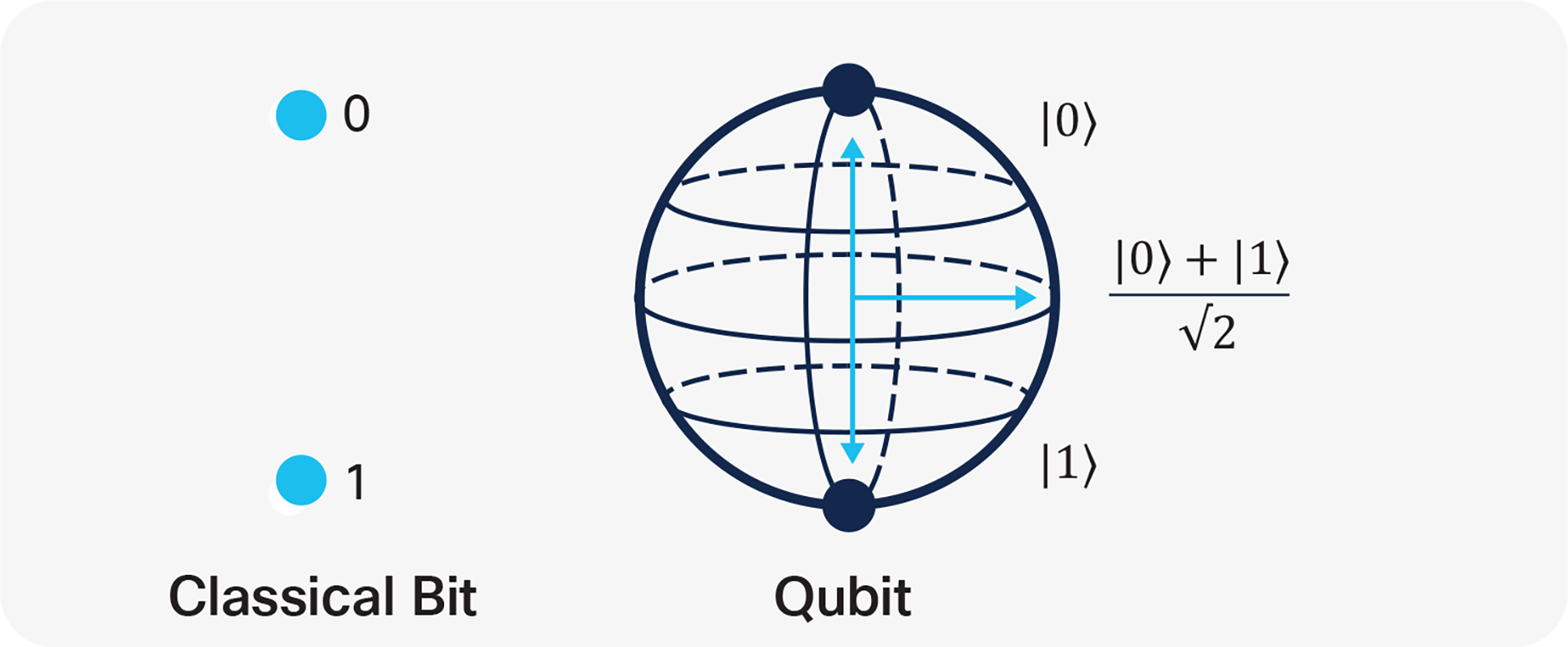
Comparison of regular bits with a qubit

A qubit state is described, according to Dirac notation, by a wave function |ψ⟩ that is the result of a combination of two basis {|0⟩, |1⟩} with two complex coefficients (α, β):

|ψ⟩ = α ⋅|0⟩ + β ⋅|1⟩

The coefficients square represents the probability to measure the corresponding base when the qubit is subject to measure in the space of the basis {|0⟩ , |1⟩ }.

The coefficients α and β must also respect:

|α|² + |β|²= 1

A single qubit state can be graphically represented as a unit vector pointing any point in a sphere surface where the two bases are the poles (Figure 1).

When a system includes more qubits, the math gets a bit more complex. As an example, a two-qubit system can be combined using the tensor product:

|ψ⟩= |V⟩ ⊗ |W⟩= | V.W⟩

If V and W are two qubits, each described in the base {|0⟩ , |1⟩}, the resulting wave function can be described as a linear combination of four bases {|00⟩, |01⟩, |10⟩, |11⟩}:

|ψ⟩ = α₁⋅|00⟩+α₂⋅|01⟩+α₃⋅|10⟩+α₄⋅|11⟩

This notation is indeed enabling the possibility to define some states that cannot be decomposed as independent qubits:

|ψ⟩≠ (a₀|0⟩+b₀|1⟩) ⊗ (a₁|0⟩+b₁|1⟩)

That substantially means that the corresponding particles cannot be described independently anymore. This property of quantum particles is called entanglement.

An example of an entangled state is the Bell state, also known as an EPR pair:

|Φ⁺⟩ = 1/√2 (|00⟩+ |11⟩)           |ψ⁺⟩ = 1/√2 (|01⟩+ |10⟩)

|Φ^-⟩ = 1/√2 (|00⟩- |11⟩)            |ψ^-⟩ = 1/√2 (|01⟩- |10⟩)

These have been pointed to by Einstein, Podolsky, and Rosen in the famous EPR paradox (1935) to claim that quantum mechanics was incomplete.

The EPR paradox, based on the assumption of local physical reality, argued that a measurement performed on one particle on a similar entangled state, which could represent a system of two noninteracting particles, cannot affect the state of the second particles as predicted by the combined state of Schrödinger’s equations.

In 1964 John Stewart Bell demonstrated that the EPR paradox conclusion was wrong; thus, the quantum theory properly describes “entangled” states of a system or rather a physical condition, where a qubit cannot be described independently any longer. So, whenever something happens to one of the qubits of an entangled system, other qubits are affected.

Now what if a computer was built out of qubits instead of bits and leveraged properties of quantum mechanics like superposition and entanglement? In the 1980s, Yuri Manin and Richard Feynman in parallel introduced the concept of the quantum computer, initially with the objective to simulate quantum phenomena to overcome the limitation of a classical computer. Since then, many potential applications emerged to tackle things like machine learning, drug discovery, and material design.

But in 1994, Peter Shor also demonstrated that the integer-factorization problem can be efficiently solved by a combination of qubit gates known as Shor’s algorithm. This substantially opened the door to break asymmetric encryption algorithms adopted in information security that rely on the complexity of problems such as factoring large numbers or computing discrete logarithms. The most likely post-quantum security scenario against the currently used cryptography standard is shown in the picture below.

Post-quantum security robustness of current standard protocols

Actual quantum computers are still in early development but the threat to communication security has triggered investigations into alternative methods to distribute encryption keys. As mentioned before, one of the methods proposed to address post-quantum security challenges is the Quantum Key Distribution (QKD) because of its theorical promise to be intrinsically unbreakable and ability to offer an easy method to detect the eavesdropper presence. Unfortunately, implementation flaws and side-channel attacks could open up a vulnerability, and while current commercial QKD systems are designed to have no exploitable implementation flaws and be resistant against known side-channel attacks, it leaves open the question about side-channel attacks that have yet to be discovered.

Cisco is collaborating on a study that uses a robust implementation of quantum key distribution based on a time-bin Measurement Device Independent (MDI-QKD) that enables the multiplexing of a quantum channel together with classical DWDM channels on the same fiber. Measurement Device Independent (MDI) QKD completely avoids the side-channel attacks on the detectors, which are the most vulnerable part of the system.

In the proposed implementation, qubits are transmitted from the endpoints Alice and Bob), using two different states to encode 0 or 1 on two different bases (time or phase) to a third party (Charlie). Charlie, who can be untrusted, performs a Bell state measurement to communicate to Bob and Alice when an entangled state is observed. Alice and Bob, knowing what they transmitted, also know what their partner states were for all entangled qubits. Measuring the Bit Error Rate (BER) on some of the received bits (key distillation), Alice and Bob can validate that the channel is secure.

But Wait, What?

Few doubt that quantum technologies will eventually yield useful and potentially disruptive products. While people in the field occasionally get distressed at how long quantum computing is taking, Robert J. Schoelkopf, an American physicist noted as one of the inventors of superconducting qubits, said “we’re going to be reaching useful quantum computations faster than people think.” Alongside government investments, hundreds of firms are investing in the field, with big names such as IBM, Google, Alibaba, Hewlett Packard, Tencent, Baidu, and Huawei all doing their own research. Google has reportedly now created a quantum computer that can solve “specialized” problems that would stump even the best classical computer.

It is believed that quantum computing will have a huge impact on areas such as logistics, military activities, pharmaceuticals (drug design and discovery), aerospace design, nuclear fusion, financial modeling, polymer design, Artificial Intelligence (AI), cybersecurity, fault detection, big data, and capital goods, especially digital manufacturing. According to an analysis by Nature, private investors have funded at least 52 quantum technology companies. The market for quantum computing is projected to reach $64.98 billion by 2030 from just $507.1 million in 2019, growing at a CAGR of 56.0 percent during the forecast period (2020–2030). According to a CIR estimate, revenue from quantum computing is pegged at $8 billion by 2027.

Will quantum key distribution be the real ultimate solution to the PKI weakness exposed by Shor’s algorithm? Probably not. Fiber optics interact with photons enough to limit the usability of a QKD, based on a single photon’s transmission. After about a few hundred kilometers, the QKD generation rate will drop heavily, or rather the error rate will become substantially indistinguishable from an attacker reading the photon. This implies that, if we need to transmit farther, either we place digital repeaters that could be susceptible to attack, or quantum untrusted repeaters (which do not exist yet); either would make the QKD solution very expensive to implement. Therefore, the search for new quantum-secure algorithms has not ceased.

As mentioned earlier, the algorithms in common use for public key encryption and signatures will be vulnerable to quantum computers, hence researchers are been developing alternative algorithms. The National Institute of Standards and Technology (NIST), responsible for cybersecurity standards, has published a list of 26 candidates for new post-quantum-secure algorithms: 17 for key exchange and 9 digital signatures.

The Post-Quantum Secure (PQ-Secure) cryptography standard is likely to have a draft available between 2022 and 2024, with the expectation that it will be adopted after 2025. Still, as shown in the picture below, PQ-Secure will likely be adopted before a scalable quantum computer for cryptanalysis will be available.

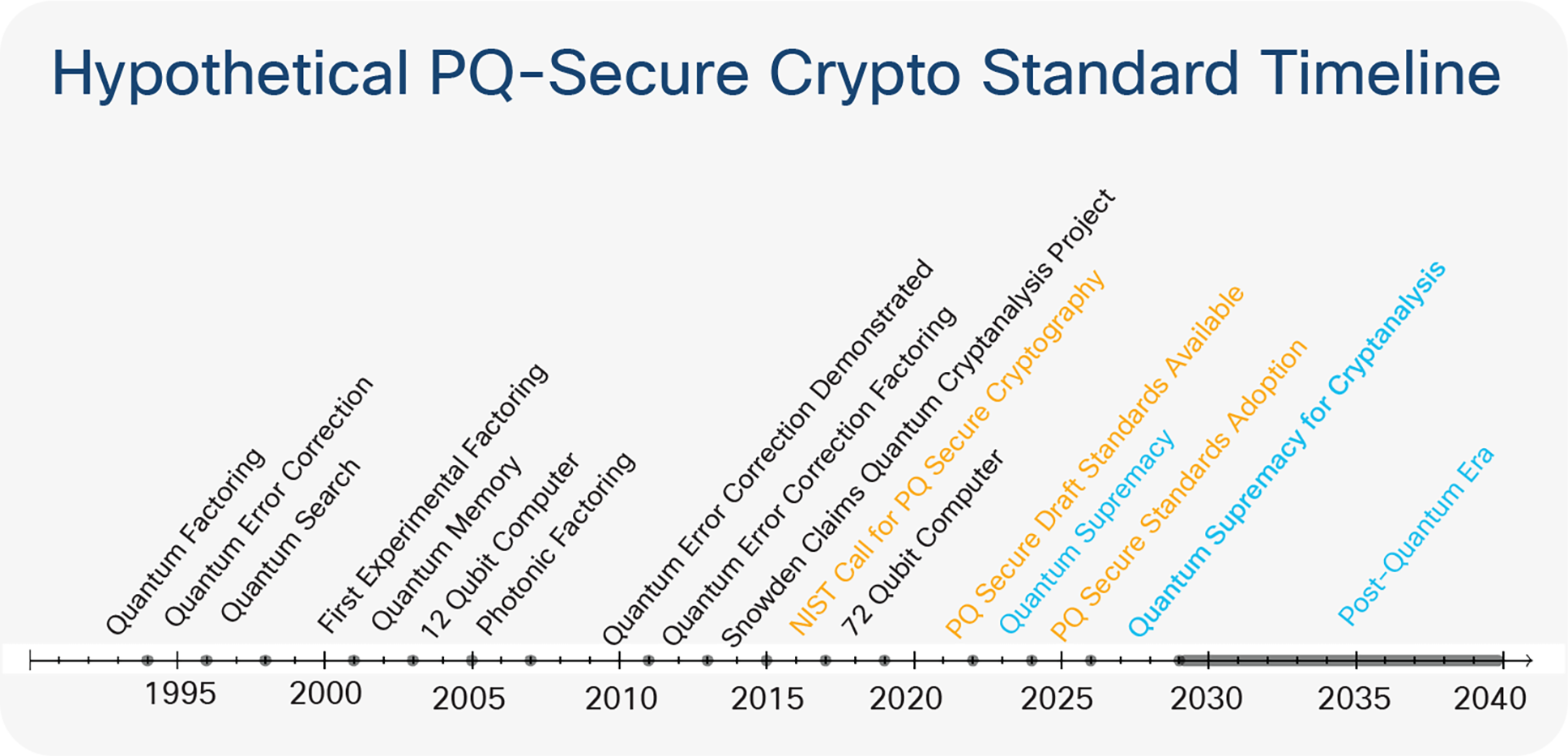
Timeline for various quantum cryptography standards

Secure Key Integration Protocol

Cisco has built a protocol called Secure Key Integration Protocol (SKIP). The SKIP protocol enables any Cisco^® router that supports encryption to use keys that are provided by a quantum distribution system. In Figure 4 there are two locations and two encrypting routers, one in each location. Each encrypting router is co-located with a key provider. The key providers communicate between themselves in the same way quantum key distribution would.

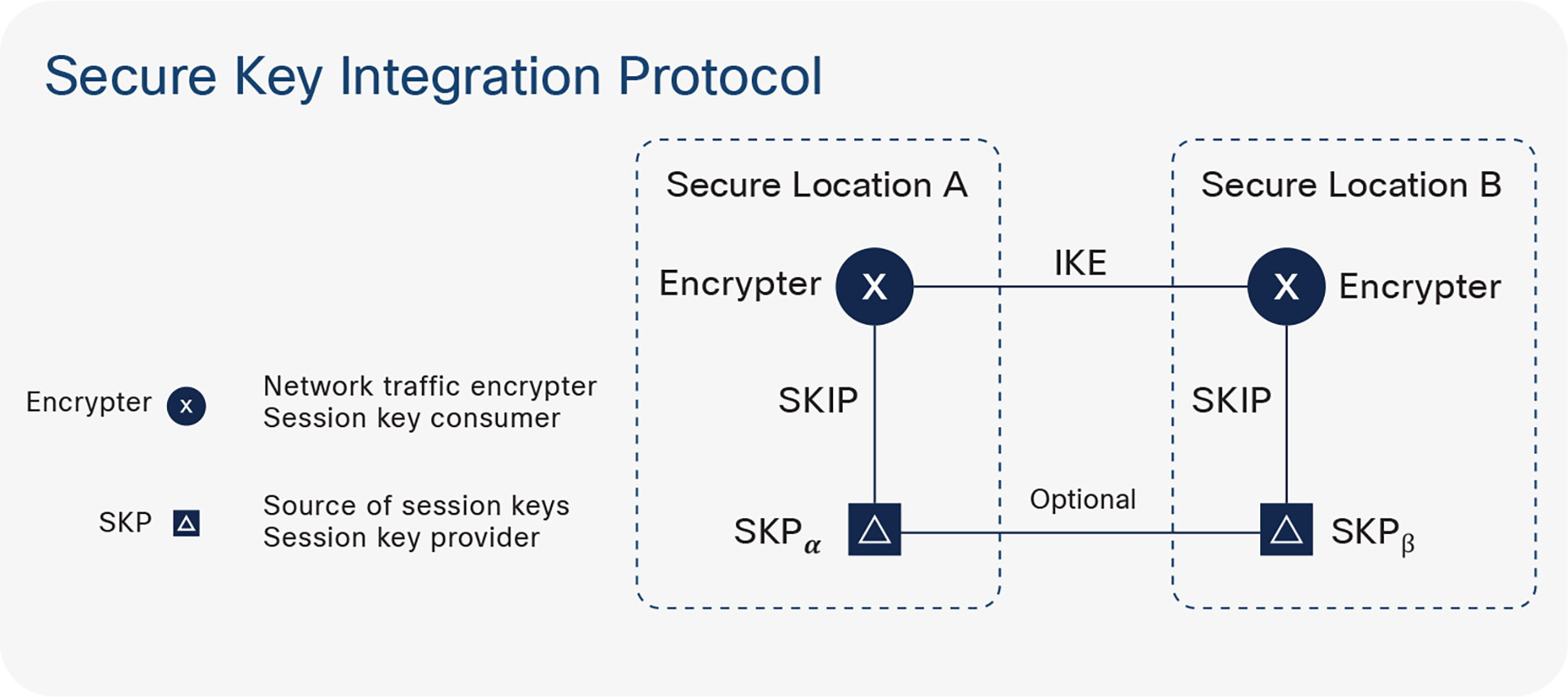
How Secure Key Integration Protocol works

When one encryption router wants to communicate with the other encrypting router, it asks its co-located key provider for a secret. It also provides an identifier back to the encrypting router, that router shares it with the other location, and the receiving router asks its own key provider for a key for the corresponding identifier.

With that solution, you can have existing router-based solutions like MacSEC or IPSec or, in principle, any cryptographic security protocol take advantage of PQ-Secure methods like QKD or preshared keys, or post-quantum-secure methods. SKIP is available today for trial if you contact your Cisco salesperson.

Conclusion

In conclusion, quantum computing definitely has the potential to break secure key exchange protocols. Nobody will argue with this. How quantum computing will scale, while quantum error correction itself is an implementation challenge, still needs to be solved. Real quantum cryptoanalysis is most likely about 10 years away. Quantum key exchange has proven fantastic and unbreakable when implemented correctly, but it is limited by the physical infrastructure. There may be a niche application for relative short distances, but it will not be a general solution. Cisco is tracking all of the solutions in this area and is bringing to market a flexible solution that will enable our customers to use whatever PQ-Secure solution they feel most appropriate for them.