Defining Analog Voice
Available Languages
Contents
Introduction
This document discusses how analog voice signals are measured, the units used, and the points of reference used when you measure.
The quality of a transmission system is defined by the difference between spoken voice at one end and reproduced voice at the other end. Anyone who uses the telephone experiences both good and bad connections, and can probably describe the quality of a particular connection in a subjective way. But how can you define good and bad quality in an objective way?
In transmission, the first step to answer this question is to decide upon these questions:
-
What is to be measured?
-
What are the measurement units?
-
What is the reference point for the measurements?
This document answers these questions.
Prerequisites
Requirements
There are no specific requirements for this document.
Components Used
This document is not restricted to specific software and hardware versions.
Conventions
Refer to the Cisco Technical Tips Conventions for more information on document conventions.
Analog Voice Characteristics
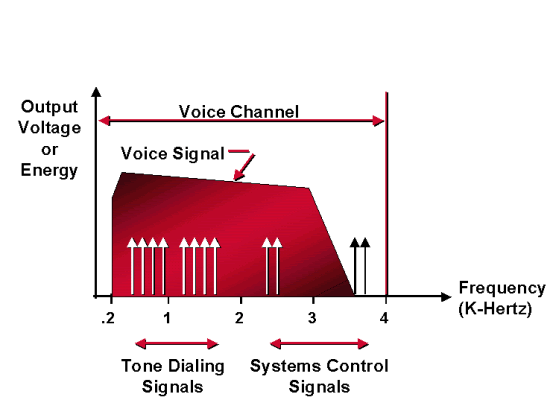
Analog is defined as a signal that has a continuously and smoothly varying amplitude or frequency. Human speech, and everything else you hear, is in analog form, and early telephone systems were analog as well. Analog signals are often depicted as smooth sine waves, but voice and other signals are more complex than that, since they contain many frequencies. The figure in the Analog Voice Measurement section shows the typical distribution of energy in voice signals.
The vertical axis is relative energy and the horizontal axis is frequency. The figure in the Analog Voice Measurement section shows that the voice frequencies that contribute to speech can extend from below 100 hertz to above 6000. However, most of the energy necessary for intelligible speech is contained in a band of frequencies between 200 and 4000.
In order to eliminate unwanted signals (noise) that can disturb conversations or cause errors in control signals, the circuits that carry the telephone signals are designed to pass only certain frequencies. The ranges of frequencies that are passed are said to be in the pass band. Zero to 4000 hertz is the pass band of a telephone system voice channel-a VF channel. (Sometimes this band is called a message channel.) Bandwidth is the difference between the upper limit and lower limit of the pass band. Therefore, the bandwidth of the VF channel is 4000 hertz. However, the transmission of speech does not require the entire VF channel. The voice pass band is restricted to 300 through 3300 hertz. Hence, any signal carried on the telephone circuit that is within the range of 300 to 3300 hertz is called an in-band signal. Any signal that is not within the 300 to 3300 hertz bands, but is within the VF channel, is called an out-of-band signal. All speech signals are in-band signals. Some signaling transmissions are in-band and some are out-of-band.
Analog Voice Measurement
Any waveform can be characterized in terms of frequencies and power. The quantities commonly used to describe various aspects of transmission performance are frequency and power. Many performance standards are stated in terms of power at a particular frequency. The unit used to measure frequency is the hertz, abbreviated as Hz or seen with the f symbol. Hertz equals one (0.00000000125) cycle or one oscillation per second and measures the waves or frequencies of electric changes each second..
As is common in most electrical systems, power is measured in units of watts, abbreviated W. Since the power encountered in transmission systems is relatively small (compared to the power of a light bulb), power is usually expressed in milliwatts, abbreviated mW.
1 mW = 1 W = 0.001W = 10–3W
————
1000
In transmission, the common interest is in power ratios rather than in absolute power. In addition, transmission is concerned with an extremely wide range of absolute power values. For these reasons, a convenient mathematical expression of relative power, the decibel (dB), is commonly used. In order to describe relative power in terms of decibels, you must define the reference point from which you measure. Based upon the transmission parameter that is measured, you can use different forms of decibel measurement. Each form of measurement has a specifically defined reference point. When you use the appropriate units of power related to specific references, you can measure absolute power, relative power, and power gains and losses.
Milliwatt and Hertz
Since the power in telephone circuits is small, the milliwatt is used as the basic power measurement unit, just as the foot is used as the basic measurement of length. Most measurements of absolute power in transmission are made in milliwatts or in units that are directly related to milliwatts.
The frequencies that are used in testing usually fall within the voice frequency band. Commonly used pure (sine wave) test tones are 404 Hz, 1004 Hz, and 2804 Hz. (The 4-Hz offset is not always stated. However, actual test frequencies should be offset by 4 Hz in order to compensate for effects that some carrier facilities have on test tones.) A measurement of 1004 Hz is near the voice-band frequencies that carry much of voice power, 404 Hz is near the low end of the spectrum, and 2804 Hz is in the range of higher-frequency components of the voice spectrum that are important to the intelligibility of speech.
In addition to pure test tones, "white noise" within specific frequency ranges is used for certain tests. White noise test tones are complex waveforms that have their power evenly distributed over the frequency range of interest. "White noise" is a signal that contains all the audio frequencies in equal amounts, but which manifests no recognizable pitches or tones
This figure illustrates, in a very general and simplified way, how a test-tone transmission is set up and how test tones are generated and measured (demarc A to demarc B).
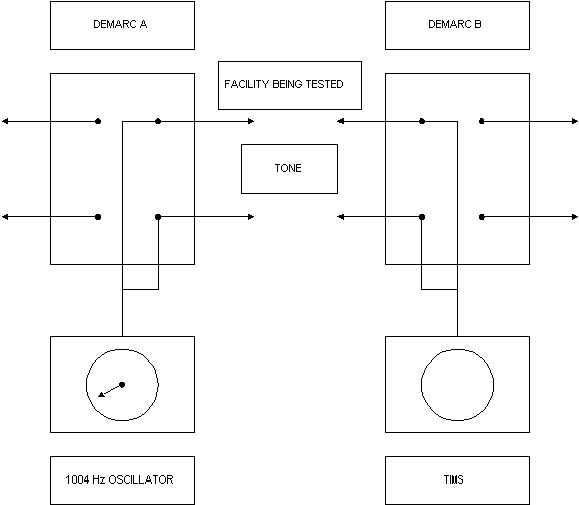
The equipment is set up to test the circuit between the demarc at A and the demarc at B. You are going to measure 1004 Hz loss inherent in the circuit between A and B.
The bridging clips at both demarcs are removed in order to isolate the segment of the circuit under test.
At A, an oscillator is attached to transmit and receive leads (also called tip and ring leads). At B, a transmission measuring set (TIMS) is attached to transmit and receive leads.
The oscillator at A is set to generate a pure test tone with a power of 1 mW at 1004 Hz. At demarc B, the TIMS is set to read power in the range of 1 mW. The power reading at B is 0.5 mW. Therefore, the power lost between A and B is:
1 mW – 0.5 mW = 0.5 mW
A more useful way to express the loss is in terms of the relative loss, or the ratio between power out (B) and power in (A):
Relative loss = Power out (B)
——————————————
Power in (A)
Relative loss = 0.5 x 10-3
——————————————
1 X 10-3
Relative loss = 0.5
Half the power that the 1004 Hz test-tone introduced at A is lost by the time
it reaches B.
This example repeats the test with the use of less test-tone power. The oscillator at demarc A is set to generate 1004 Hz tone at a power of 0.1 mW. At demarc B, the power measurement is 0.05 mW. Then, the absolute power loss is:
0.1 mW – 0.05 mW = 0.05 mW
The relative loss, or the ratio between power out (B) and power in (A), is:
Relative Loss = Power out(B)
——————————————
Power in (A)
Relative Loss = 0.05 x 10-3
—————————————
1 x 10-3
Relative Loss = 0.5
The relative loss, or power ratio between B and A, is the same whether you use a test signal of 1 mW or 0.1 mw.
The Decibel
Mathematically, the decibel is a logarithmic measure. The logarithm, or log, of a particular number is the mathematical power to which a base number must be raised in order to result in the particular number. The base number you use when you deal with the decibel is 10. For example, what is the logarithm (log) of 100? Another way to ask this question is 'To what power do you raise 10 to get 100?'. The answer is 2 because 10 x 10 = 100.
Similarly,
log (100)= 2
log (1000)= 3
log (10,000)= 4
and so on.
You can also use logarithms to express fractional quantities. For example, what is the logarithm of 0.001? Another way to ask this question is 'To what power do you raise 1/10 (0.1) to get 0.001?'. The answer is 3. By convention, the log of a fractional number is expressed as negative.
log (0.001) = -3
Logarithms of numbers that are not integral powers of 10 can be calculated when you look them up in a table or when you use a hand calculator.
The decibel uses logarithms to express power ratios. By definition, the deciBel, or dB, is the logarithmic (base 10) ratio of two powers, P1 and P2 given by:
dB = 10 log P2
——
P1
P2 and P1 are power measurements expressed in consistent units. The number of decibels is positive if P2 is greater that P1. The number is negative if P1 is greater that P2 (see the table). It is important that the two powers be expressed in the same units, such as milliWatt (mW) or Watt (W). Otherwise, this leads to errors in calculation.
| Power Ratio | dB Value |
|---|---|
| 2 | 3* |
| 4 | 6* |
| 8 | 9* |
| 10 | 10 |
| 100 | 20 |
| 1000 | 30 |
| 100000 | 50 |
| 1000000000 | 90 |
* Approximate dB value.
The power ratio between the power measured at B and the power measured at A was one-half. Expressed in decibels:
(Loss, A to B) = 10 log (0.5) (Loss, A to B) = –3 dB
With the use of decibels, you can express the loss or gain of a circuit or piece of equipment without having to explicitly state the actual values of the input and output power. In the example, the loss between A and B is always 3 dB, regardless of the absolute amount of power that is transmitted.
Decibel Measurement Relative to One Milliwatt
Absolute power is expressed in milliwatts and relative power is expressed in decibels. When you establish a relationship between the decibel and the milliwatt, you can eliminate the milliwatt as an operational unit of measure and deal exclusively with the decibel and related units of measure. The unit of measure that is used to express absolute power in terms of decibels is dBm.
dBm = 10 log (Power, measured in mW)
—————————————————————————
1 mW
Since a milliwatt is the standard power reference in communications, it is logical that 0 dBm (the absolute power reference when decibel units are used) is equal to 1 mW of power. Mathematically:
0 dBm = 10 log Power out
——————————
Power in
0 dBm = 10 log (1/1)
0 dBm = 10 x 0 = 0
Because the power is an alternating current waveform and impedance can vary as a function of frequency, it is necessary to state what frequency the 0 dBm standard is based upon. The standard frequency is 1004 Hz.
You must also know the resistance or impedance (load) of the circuit. The standard impedance is 600 Ohms.
Therefore, the reference of 0 dBm is equal to 1 mW of power imposed upon an impedance of 600 Ohms of a frequency of 1004 Hz.
Tests are usually performed with the use of test signals that are less powerful than 1 mW (0 dBm). If you apply a 1004 Hz test tone of –13 dBm at A, you read –16 dBm on the TIMS at B. The loss is still –3 dB.
Transmission Level Point
In any discussion of the performance of a circuit, it is necessary to describe the power at a particular point in a circuit with reference to the power present at other points in the circuit. This power can be signal power, noise, or test tones.
The description of this power is similar to the description of the height of a mountain (or the depth of the ocean). In order to measure the height of a mountain, it is necessary to pick a reference height from which to measure. The standard reference height is sea level, which is arbitrarily assigned a height of zero. When you measure all mountains from sea level, comparisons of their height can be made even though they can be many miles apart.
This figure shows test tone transmission from demarc A to demarc B.

In a similar manner, power, at specified points in a circuit, can be described in terms of the power at a standard reference point.
This point, which is analogous to sea level, is called the zero transmission level point, or 0 TLP.
Any other TLP can be referenced to the 0 TLP by algebraically summing the 1004 Hz gains and losses from the 0 TLP to the point of measurement.
The power present at a particular point in a circuit depends on the power at the signal source, on where the source is applied, and on the loss or gain between the two points in question.
With the use of the 0 TLP concept, the power in a circuit is described by stating what the power would be if it were accurately measured at the 0 TLP. The standard notation is dBm0, which means power referenced to the 0 TLP.
For example, the term –13 dBm0 means that the power at the 0 TLP is –13 dBm. A TIMS that is properly set up measures –13 dBm at the 0 TLP. An example of a –13 dBm0 signal.
Once the power at the 0 TLP is found, the power at any other point in the circuit can easily be determined. For example, if the signal is –13 dBm when measured at the 0 TLP, it is l3 dB below the numeric value of any TLP on the circuit when measured at that TLP.
If the signal is –13 dBm at the 0 TLP (makes it a –13-dBm0 signal), then the power at the +5 TLP can be calculated as this output shows:
(TLP) + (Power at the 0 TLP) = Power at the +5 TLP) (+5)+(–13 dBm0) = –8 dBm
If the –13-dBm0 signal is properly measured at the +5 TLP, the meter reads –8 dBm.
In a similar manner, if a –13-dBm0 signal is measured at the –3 TLP, the meter reads –16 dBm:
(TLP) + (Power at the 0 TLP) = (Power at the –3 TLP) (–3)+(–13 dBm0) = –16 dBm
In order to determine the expected power at any given TLP, it is sufficient to know the power present at some other TLP in the circuit. And, just as the mountain does not have to be near the sea in order to determine its height, the 0 TLP does not have to actually exist on the circuit.
This figure illustrates a circuit between two demarcs. A –29-dBm test-tone signal is applied at the –16 TLP. What should you expect to measure at the +7 TLP?
Even though the 0 TLP does not exist on the circuit, you can describe the power you see at the 0 TLP if it did exist:
TLP)+(Power at 0 TLP) = (Power at the –16 TLP)
(–16)+(Power at 0 TLP) = –29 dBm
(Power at 0 TLP) = –13 dBm
Using the relationship again, you can determine the power at the + 7 TLP:
(TLP)+ (Power at 0 TLP) = (Power at + 7 TLP) (+7)+(–13 dBm0) = –6 dBm
Use of the 0 TLP reference permits transmission objectives and measured results to be stated independently of any specific TLP, and without the specification of what the test-tone levels are to be or where the test tone is to be applied.
This figure shows a test tone transmission from demarc A to demarc B.

Noise Measurement Units
In addition to the description of test-tone power at various points in a circuit, decibel-related units of measure can be used to describe noise present in a circuit.
dBrn
In order to describe power in a circuit, the term dBm is used, meaning "power referenced to 1 mW." Since noise typically contains much less than 1 mW of power, it is convenient to use a reference power that is much smaller than 1 mW. The reference power used in the description of noise is –90 dBm. The notation used to describe noise in terms of reference noise is dBrn. If you know the noise level in dBm, you can easily measure the noise in dBrn:
dBrn = dBm + 90 dB
For example, a noise measurement of 30 dBrn indicates a power level of –60 dBm (30 dB above the –90 dBm reference noise level). This table shows the relationship between dBm0 and dBrn.
| dBm0 | dB Value |
|---|---|
| 0 | 90 |
| -10 | 80 |
| -20 | 70 |
| -30 | 60 |
| -40 | 50 |
| -50 | 40 |
| -60 | 30 |
| -70 | 20 |
| -80 | 10 |
| -90 | 0 |
DBrnC
Noise contains numerous irregular waveforms that have a wide range of frequencies and powers. Although any noise superimposed upon a conversation has an interfering effect, experiments have shown that the interfering effect is greatest in the midrange of the voice frequency band.
In order to obtain a useful measure of the interfering effect of noise, the various frequencies that contribute to the overall noise are weighted based on their relative interfering effect. This weighting is accomplished through the use of weighting networks, or filters, within TIMS.
Noise measurements through a C-message weighting network are expressed in units of dBrnC (noise above reference noise, C-message weighting).
DBrnCO
As with test-tone power, noise power can be referenced to the 0 TLP.
For example, if the noise objective for the circuit is 31 dBrnC0, what is the noise measurement at the +7 TLP?
TLP) + (Noise at the 0 TLP) = (Noise at TLP)
(+7) + (31 dBrnC0) = 38 dBrnC
The noise measurement at the +7 TLP is 38 dBrnC.
What is the noise measurement at the –16 TLP?
(TLP) + (Noise at the 0 TLP) = (Noise at TLP)
(–16) + (31 dBrnC0) = 15 dBrnC
The noise measurement at the –16 TLP is 15 dBrnC.
Related Information
Contact Cisco
- Open a Support Case

- (Requires a Cisco Service Contract)
 Feedback
Feedback