Introduction to Optical Fibers, dB, Attenuation and Measurements
Available Languages
Contents
Introduction
This document is a quick reference to some of the formulas and important information related to optical technologies. This document focuses on decibels (dB), decibels per milliwatt (dBm), attenuation and measurements, and provides an introduction to optical fibers.
Prerequisites
Requirements
There are no specific requirements for this document.
Components Used
This document is not restricted to specific software and hardware versions.
The information in this document was created from the devices in a specific lab environment. All of the devices used in this document started with a cleared (default) configuration. If your network is live, make sure that you understand the potential impact of any command.
Conventions
Refer to Cisco Technical Tips Conventions for more information on document conventions.
What is a Decibel?
A decibel (dB) is a unit used to express relative differences in signal strength. A decibel is expressed as the base 10 logarithm of the ratio of the power of two signals, as shown here:
dB = 10 x Log10 (P1/P2)
where Log10 is the base 10 logarithm, and P1 and P2 are the powers to be compared.
Note: Log10 is different from the Neparian Logarithm (Ln or LN) base e logarithm.
You can also express signal amplitude in dB. Power is proportional to the square of the amplitude of a signal. Therefore, dB is expressed as:
dB = 20 x Log10 (V1/V2)
where V1 and V2 are the amplitudes to be compared.
1 Bell (not currently used) = Log10 (P1/P2)
1 decibel (dB) = 1 Bell / 10 = 10 * Log10 (P1/P2)
dBr = dB (relative) = dB = 10 * Log10 (P1/P2)
Base 10 Logarithm Rules
-
Log10 (AxB) = Log10 (A) + Log10 (B)
-
Log10 (A/B) = Log10 (A) - Log10 (B)
-
Log10 (1/A) = - Log10 (A)
-
Log10 (0,01) = - Log10 (100) = -2
-
Log10 (0,1) = - Log10(10) = - 1
-
Log10 (1) = 0
-
Log10 (2) = 0,3
-
Log10 (4) = 0,6
-
Log10 (10) = 1
-
Log10 (20) = 1,3
Log10 (2 x 10) = Log10 (2) + Log10 (10) = 1 + 0,3
-
Log10 (100) = 2
-
Log10 (1000) = 3
-
Log10 (10000) = 4
dB
This table lists the Logarithm and dB (decibel) power ratios:
| Power Ratio | dB = 10 x Log10 (Power Ratio) |
|---|---|
| AxB | x dB = 10 x Log10(A) + 10 x Log10(B) |
| A/B | x dB = 10 x Log10(A) - 10 x Log10(B) |
| 1/A | x dB = + 10 x Log10 (1/A) = - 10 x Log10 (A) |
| 0,01 | - 20 dB = - 10 x Log10(100) |
| 0,1 | - 10 dB = 10 x Log10 (1) |
| 1 | 0 dB = 10 x Log10 (1) |
| 2 | 3 dB = 10 x Log10 (2) |
| 4 | 6 dB = 10 x Log10 (4) |
| 10 | 10 dB = 10 x Log10 (10) |
| 20 | 13 dB = 10 x (Log10 (10) + Log10 (2)) |
| 100 | 20 dB = 10 x Log10 (100) |
| 1000 | 30 dB = 10 x Log10 (1000) |
| 10000 | 40 dB = 10 x Log10 (10000) |
Decibels in Milliwatts (dBm)
dBm = dB milliwatt = 10 x Log10 (Power in mW / 1 mW)
| Power | Ratio | dBm = 10 x Log10 (Power in mW / 1 mW) |
|---|---|---|
| 1 mW | 1 mW/1mW=1 | 0 dBm = 10 x Log10 (1) |
| 2 mW | 2 mW/1mW=2 | 3 dBm = 10 x Log10 (2) |
| 4 mW | 4 mW/1mW=4 | 6 dBm = 10 x Log10 (4) |
| 10 mW | 10 mW/1mW=10 | 10 dBm = 10 x Log10 (10) |
| 0,1 W | 100 mW/1mW=100 | 20 dBm = 10 x Log10 (100) |
| 1 W | 1000 mW/1mW=1000 | 30 dBm = 10 x Log10 (1000) |
| 10 W | 10000mW/1mW=10000 | 40 dBm = 10 x Log10 (10000) |
Decibels that Reference One Watt (dBW)
dBW = dB Watt = 10 x Log10 (Power in W / 1 W)
| Power | Ratio | dBm = 10 x Log10 (Power in mW / 1 mW) |
|---|---|---|
| 1 W | 1 W / 1 W = 1 | 0 dBW = 10 x Log10 (1) |
| 2 W | 2 W / 1 W = 2 | 3 dBW = 10 x Log10 (2) |
| 4 W | 4 W / 1 W = 4 | 6 dBW = 10 x Log10 (4) |
| 10 W | 10 W / 1 W = 10 | 10 dBW = 10 x Log10 (10) |
| 100 mW | 0,1 W / 1 W = 0,1 | -10 dBW = -10 x Log10 (10) |
| 10 mW | 0,01 W / 1 W = 1/100 | -20 dBW = -10 x Log10 (100) |
| 1 mW | 0,001W/1W=1/1000 | -30 dBW = -10 x Log10 (1000) |
Power/Voltage Gains
This table compares the power and voltage gains:
| dB | Power Ratio | Voltage Ratio | dB | Power Ratio | Voltage Ratio |
|---|---|---|---|---|---|
| 0 | 1,00 | 1,00 | 10 | 10,00 | 3,16 |
| 1 | 1,26 | 1,12 | 11 | 12,59 | 3,55 |
| 2 | 1,58 | 1,26 | 12 | 15,85 | 3,98 |
| 3 | 2,00 | 1,41 | 13 | 19,95 | 4,47 |
| 4 | 2,51 | 1,58 | 14 | 25,12 | 5,01 |
| 5 | 3,16 | 1,78 | 15 | 31,62 | 5,62 |
| 6 | 3,98 | 2,00 | 16 | 39,81 | 6,31 |
| 7 | 5,01 | 2,24 | 17 | 50,12 | 7,08 |
| 8 | 6,31 | 2,51 | 18 | 63,10 | 7,94 |
| 9 | 7,94 | 2,82 | 19 | 79,43 | 8,91 |
| 10 | 10,00 | 3,16 | 20 | 100,00 | 10,00 |
With this information, you can define the formulas for attenuation and gain:
Attenuation (dB) = 10 x Log10(P in/P out) = 20xLog10(V in/V out)
Gain (dB) = 10 x Log10(P out/P in) = 20 x Log10(V out/V in)
Optical Fiber Structure
Optical fiber is a medium to carry information. Optical fiber is made of silica-based glass, and consists of a core surrounded by cladding. The central part of the fiber, called the core, has a refractive index of N1. The cladding that surrounds the core has a lower refractive index of N2. When light enters the fiber, the cladding confines the light to the fiber core, and the light travels down the fiber by internal reflection between the boundaries of the core and the cladding.
Figure 1 – Optical Fiber Structure 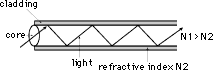
Fiber Type
Singlemode (SM) and multimode (MM) fibers are the mainstream fibers that are manufactured and marketed today. Figure 2 provides information on both these fiber types.
Figure 2 – SM and MM Fibers 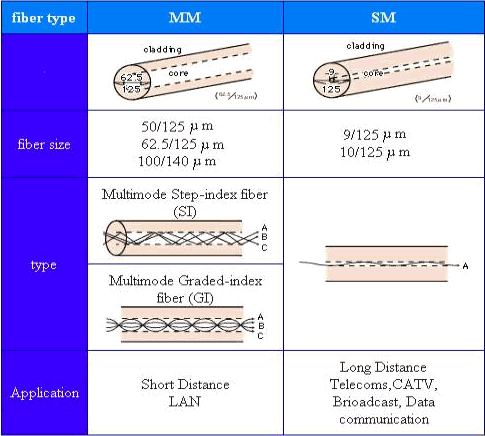
Wavelength
A small amount of light is injected into the fiber. This falls into visible wavelength (from 400nm to 700nm) and near infrared wavelength (from 700nm to 1700nm) in the electromagnetic spectrum (see Figure 3).
Figure 3 – The Electromagnetic Spectrum 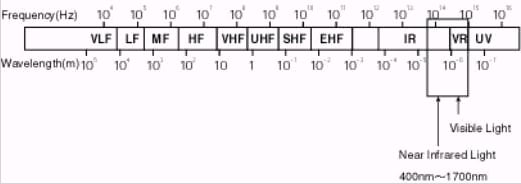
There are four special wavelengths that you can use for fiber optic transmission with low optical loss levels, which this table lists:
| Windows | Wavelength | Loss |
|---|---|---|
| 1st wavelength | 850nm | 3dB/km |
| 2nd wavelength | 1310nm | 0.4dB/km |
| 3rd wavelength | 1550nm (C band) | 0.2dB/km |
| 4th wavelength | 1625nm (L band) | 0.2dB/km |
Optical Power
In order to measure optical loss, you can use two units, namely, dBm and dB. While dBm is the actual power level represented in milliwatts, dB (decibel) is the difference between the powers.
Figure 4 – How to Measure Optical Power 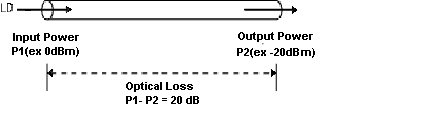
If the optical input power is P1 (dBm) and the optical output power is P2 (dBm), the power loss is P1 - P2 dB. In order to see how much power is lost between input and output, refer to the dB value in this power conversion table:
| dB | Power Out as a % of Power In | % of Power lost | Remarks |
|---|---|---|---|
| 1 | 79% | 21% | - |
| 2 | 63% | 37% | - |
| 3 | 50% | 50% | 1/2 the power |
| 4 | 40% | 60% | - |
| 5 | 32% | 68% | - |
| 6 | 25% | 75% | 1/4 the power |
| 7 | 20% | 80% | 1/5 the power |
| 8 | 16% | 84% | 1/6 the power |
| 9 | 12% | 88% | 1/8 the power |
| 10 | 10% | 90% | 1/10 the power |
| 11 | 8% | 92% | 1/12 the power |
| 12 | 6.3% | 93.7% | 1/16 the power |
| 13 | 5% | 95% | 1/20 the power |
| 14 | 4% | 96% | 1/25 the power |
| 15 | 3.2% | 96.8% | 1/30 the power |
For example, when direct line (LD) optical input into the fiber is 0dBm and output power is -15dBm, optical loss for the fiber is calculated as:
Input Output Optical Loss 0dBm - (-15dBm) =15dB
In the power conversion table, 15dB for optical loss equals 96.8 percent of lost optical power. Therefore, only 3.2 percent of optical power remains when it travels through the fiber.
Understand Insertion Loss
In any fiber optic interconnection, some loss occurs. Insertion loss for a connector or splice is the difference in power that you see when you insert the device into the system. For example, take a length of fiber and measure the optical power through the fiber. Note the reading (P1). Now cut the fiber in half, terminate the fibers and connect them, and measure the power again. Note the second reading (P2). The difference between the first reading (P1) and the second (P2) is the insertion loss, or the loss of optical power that occurs when you insert the connector into the line. This is measured as:
IL (dB) = 10 Log10 (P2 / P1)
You must understand these two important things about insertion loss:
-
The specified insertion loss is for identical fibers.
If the core diameter (or the NA) of the side that transmits data is larger than the NA of the fiber that receives data, there is additional loss.
Ldia = 10 Log10 (diar/diat)2
LNA = 10 Log10 (NAr/NAt)2
where:
-
Ldia = Loss diameter
-
diar = diameter receive
-
diat = diameter transmit
-
LNA = Loss on optical fiber
Additional loss can occur from Fresnel reflections. These occur when two fibers are separated so that a discontinuity exists in the refractive index. For two glass fibers separated by an air gap, Fresnel reflections are 0.32 dB.
-
-
The loss depends on the launch.
The insertion loss depends on the launch, and receives conditions in the two fibers that are joined. In a short launch, you can overfill the fiber with optical energy carried in both the cladding and core. Over distance, this excess energy is lost until the fiber reaches a condition known as equilibrium mode distribution (EMD). In a long launch, the fiber has already reached EMD, so the excess energy is already stripped away and is not present at the connector.
Light that crosses the fiber-to-fiber junction of an interconnection can again overfill the fiber with excess cladding modes. These are quickly lost. This is the short-receive condition. If you measure the power output of a short-receive fiber, you can see extra energy. However, the extra energy is not propagated far. The reading is therefore incorrect. Similarly, if the length of the receive fiber is long enough to reach EMD, the insertion loss reading can be higher, but it reflects actual application conditions.
You can easily simulate EMD (long launch and receive). For this, you must wrap the fiber around a mandrel five times. This strips the cladding modes.
Calculate a Power Budget
You can make a rough estimate of a link power budget. For this, you must allow 0.75 dB for each fiber-to-fiber connection, and assume that fiber loss is proportional with length in the fiber.
For a 100-meter run with three patch panels and 62.5/125 fiber that have a loss of 3.5 dB/km, the total loss is 2.6 dB, as shown here:
Fiber: 3.5 dB/km = 0.35 dB for 100 meters
Patch Panel 1 = 0.75 dB
Patch Panel 2 = 0.75 dB
Patch Panel 3 = 0.75 dB
Total = 2.6 dB
The measured loss is normally less. For example, the average insertion loss for an AMP SC connector is 0.3 dB. In this case, the link loss is only 1.4 dB. Regardless of whether you run Ethernet at 10 Mbps or ATM at 155 Mbps, the loss is the same.
Optical time-domain reflectometry (OTDR) is a popular certification method for fiber systems. The OTDR injects light into the fiber, and then graphically displays the results of detected back-reflected light. The OTDR measures elapsed transit time of reflected light to calculate the distance to different events. The visual display allows determination of loss per unit length, evaluation of splices and connectors, and fault location. OTDR zooms in to certain locations for a close-up picture of portions of the link.
While you can use power meters and signal injectors for many link certifications and evaluations, OTDRs provide a powerful diagnostic tool to get a comprehensive picture of the link. But OTDR requires more training and some skill to interpret the display.
Related Information
Revision History
| Revision | Publish Date | Comments |
|---|---|---|
1.0 |
20-Apr-2005 |
Initial Release |
Contact Cisco
- Open a Support Case

- (Requires a Cisco Service Contract)
 Feedback
Feedback